LSM树

诞生原因

传统关系型数据库使用btree或一些变体作为存储结构，能高效进行查找。但保存在磁盘中时它也有一个明显的缺陷，那就是逻辑上相离很近但物理却可能相隔很远，这就可能造成大量的磁盘随机读写。随机读写比顺序读写慢很多，为了提升IO性能，我们需要一种能将随机操作变为顺序操作的机制，于是便有了LSM树。LSM树能让我们进行顺序写磁盘，从而大幅提升写操作，作为代价的是牺牲了一些读性能。

LSM树原理

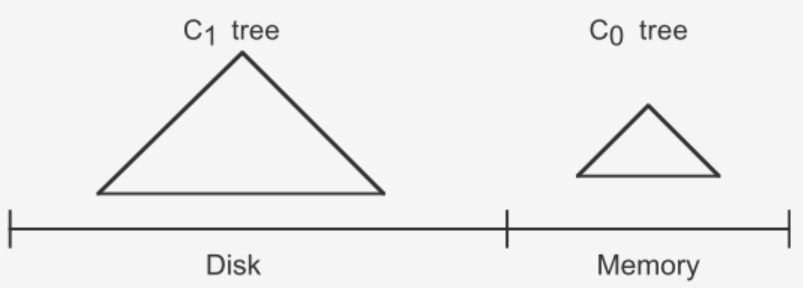
LSM树由两个或以上的存储结构组成。为了说明简单，我们用两个存储结构来说明。一个存储结构常驻内存，称为C0 tree可以是任意方便键值对查找的数据结构，例如map，红黑树等；另一个存储结构常驻硬盘，类似B+树，C1的所有节点都是满的，节点大小等于磁盘块大小。

插入步骤

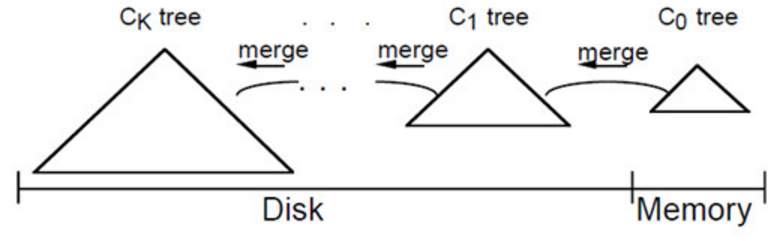
大体思路：插入一条记录时，先插入一条日志到末尾（append）。然后数据先插入到C0，因为是存储在内存中，所以是不涉及IO的；然后当C0 大小达到一个阈值，将C0记录滚动合并到C1中；对于多个存储结构，则逐层向上合并。

示例

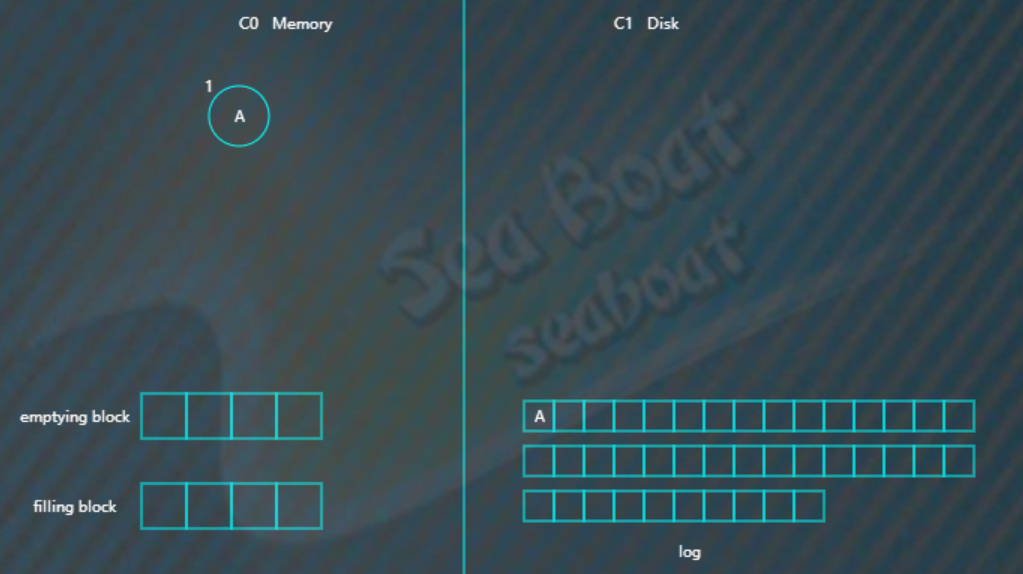
这里C0树使用AVL树，插入A，日志文件追加记录，再插入C0

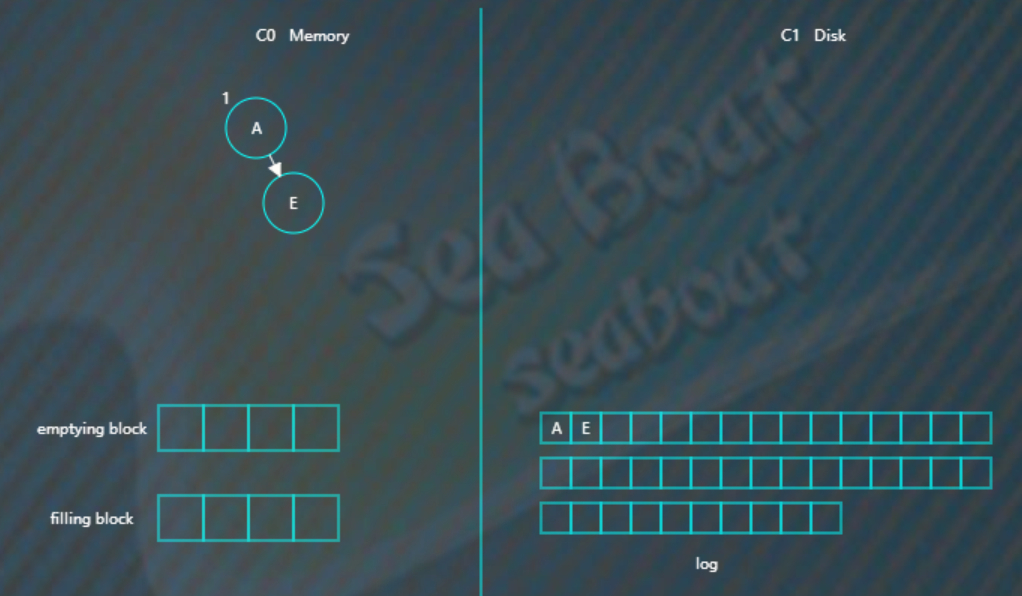
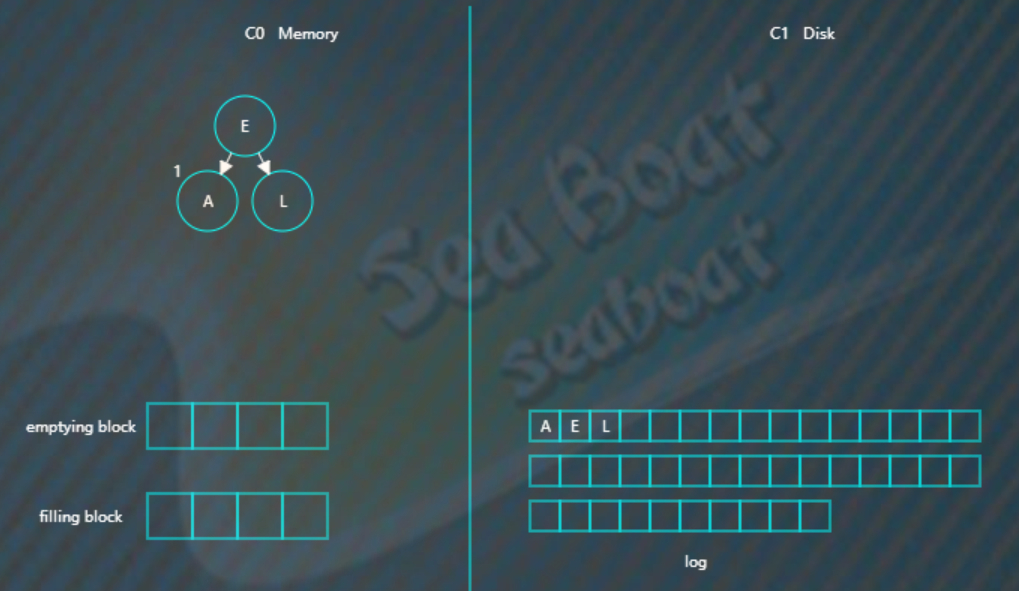
插入E

插入L

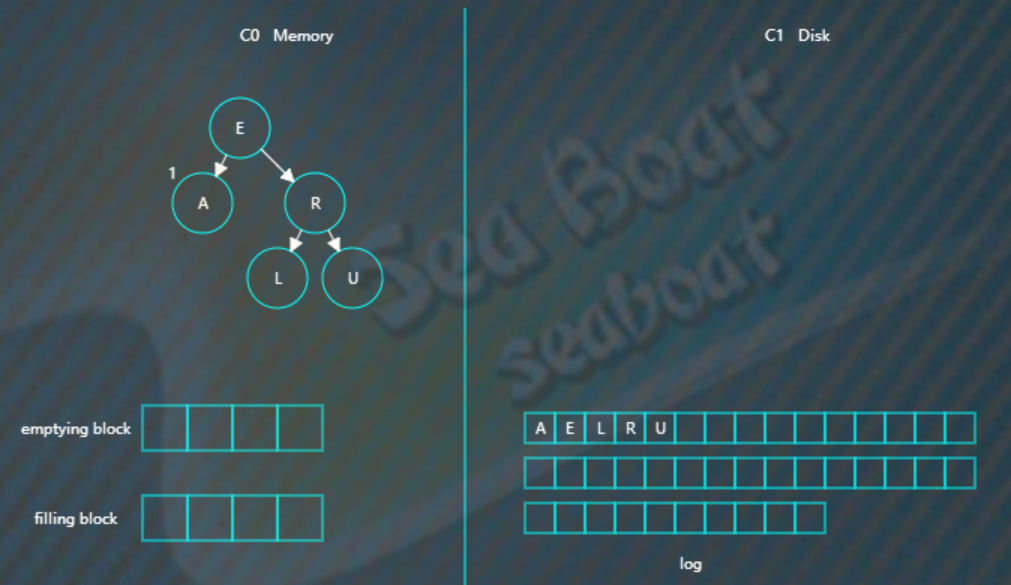
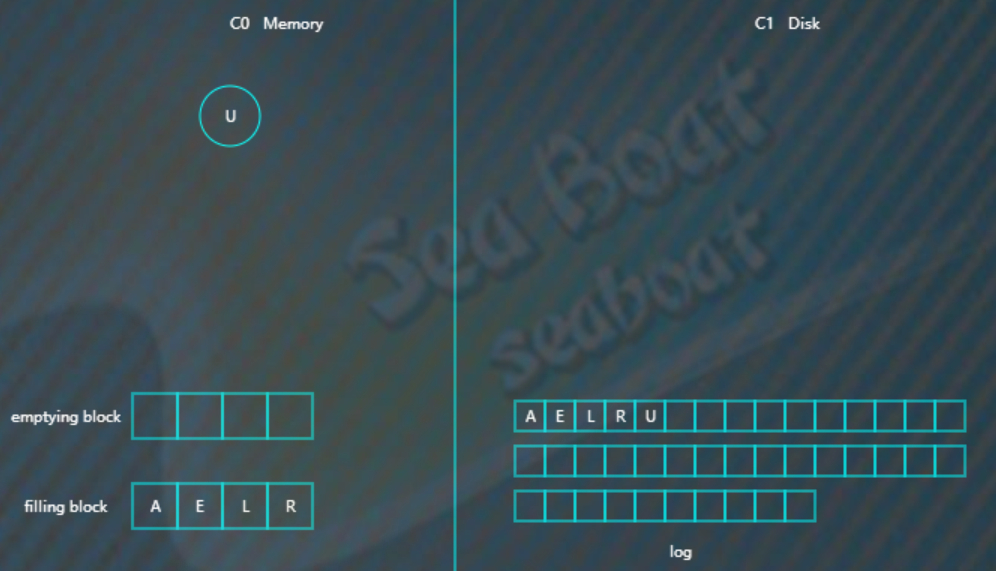
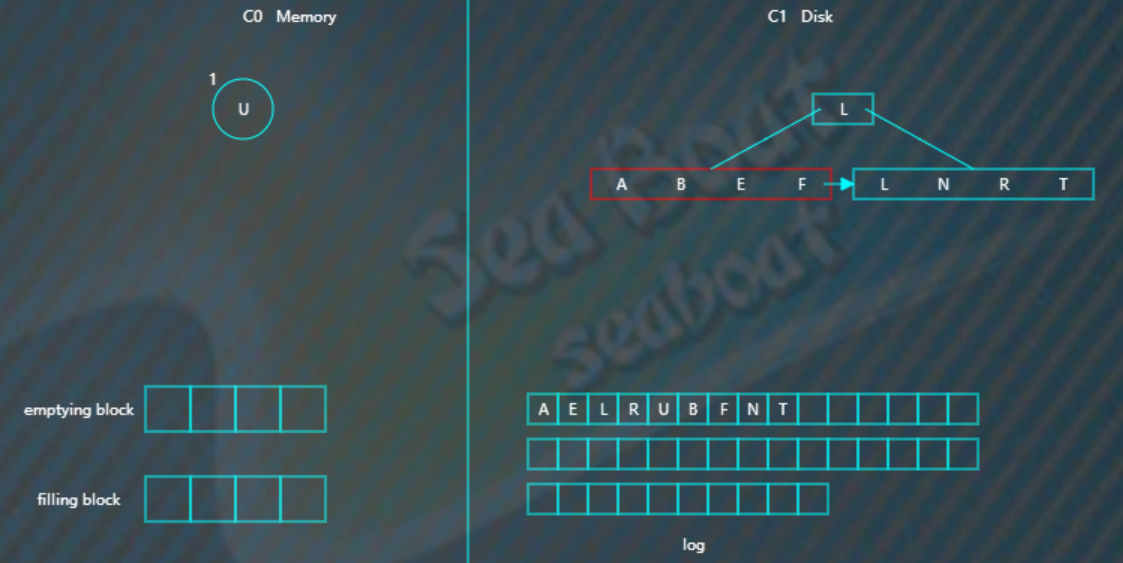
插入“R”“U”，旋转后最终如下。

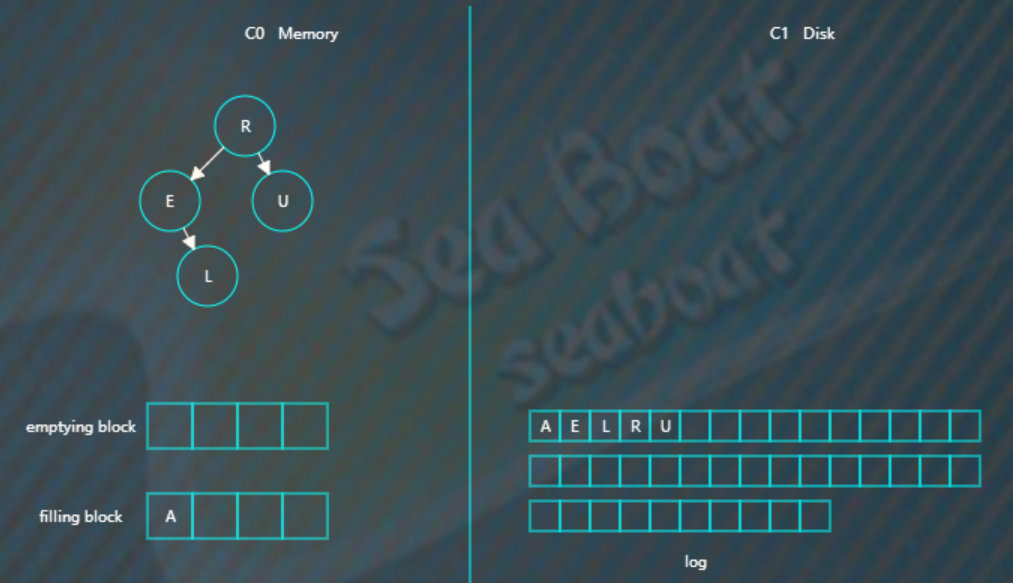
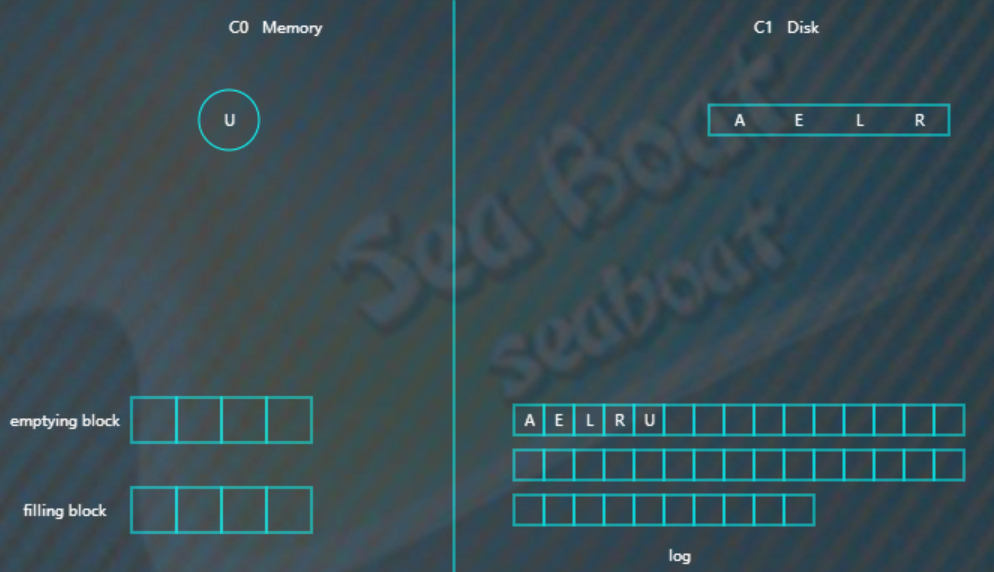
假如此时触发合并，因为C1还没有树，所以emptying block为空，直接从C0树从小到大依次找节点，放到filling blcok。

放入最小节点A。

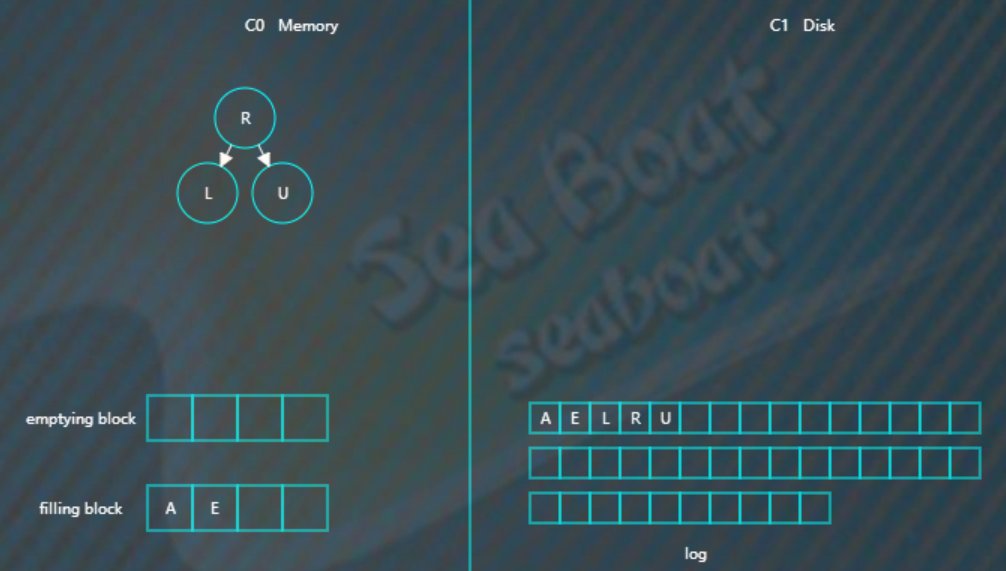
第二小节点E

如此类推直到填满filling blcok

写入C1（B+树）

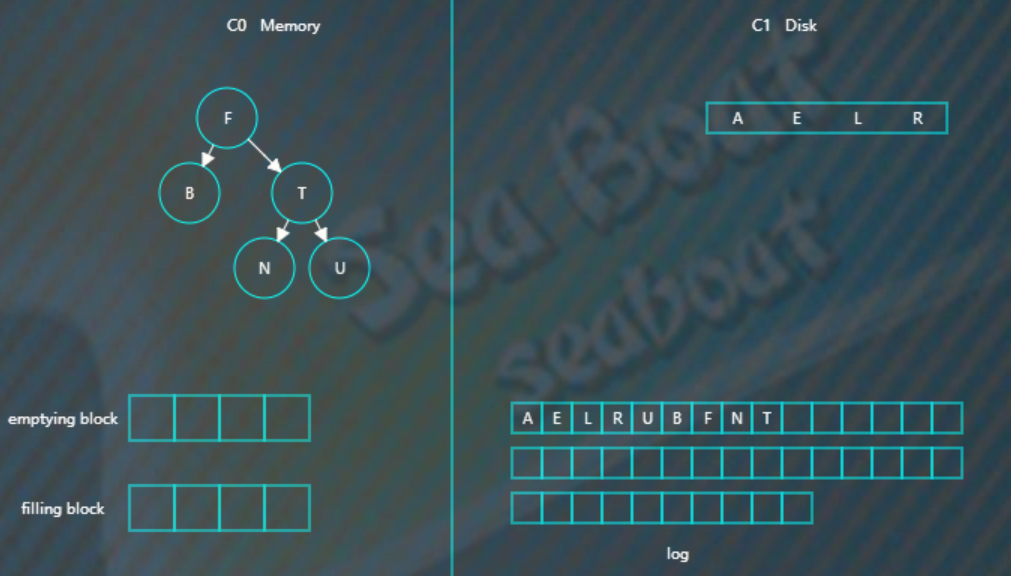
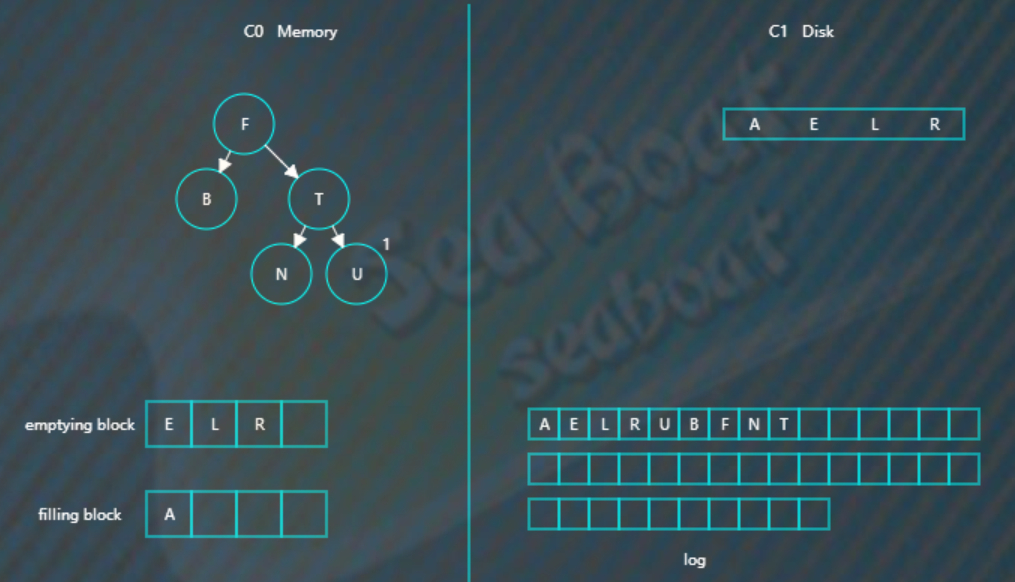
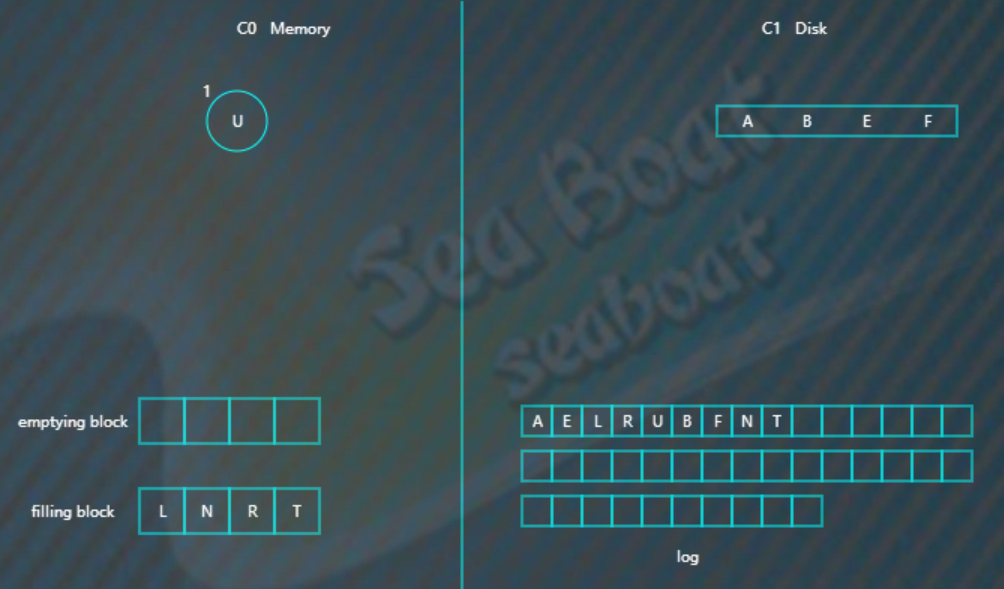
继续插入B F N T，先分别写日志，然后插入到内存的C0树中，

假如此时触发合并，先加载C1的最左节点（最小）到emptying blcok

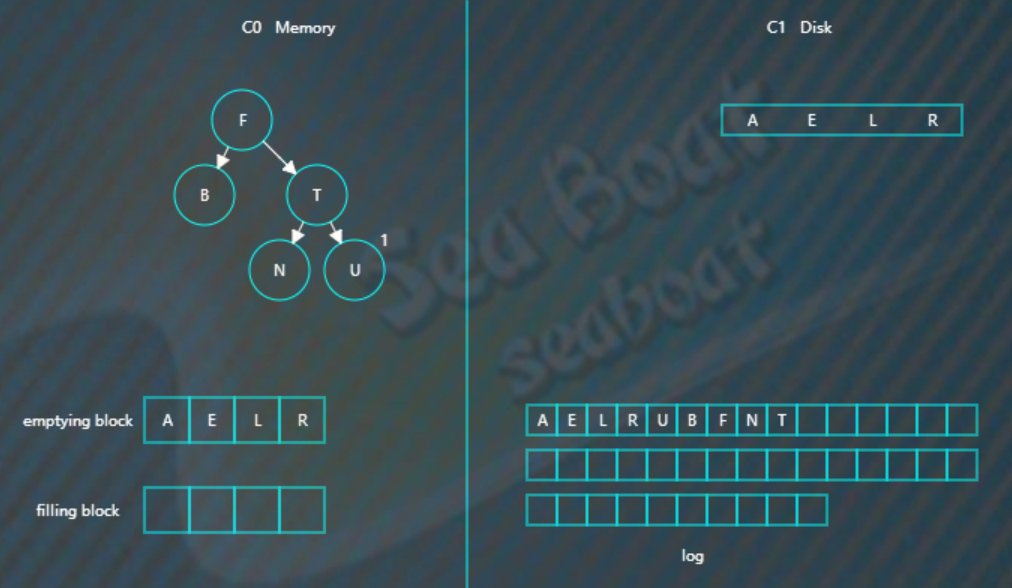
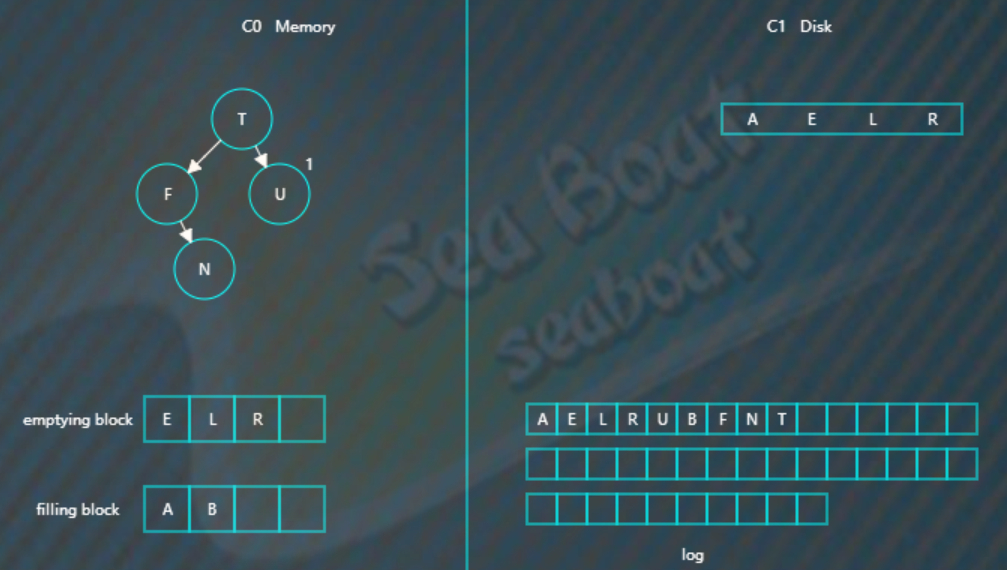
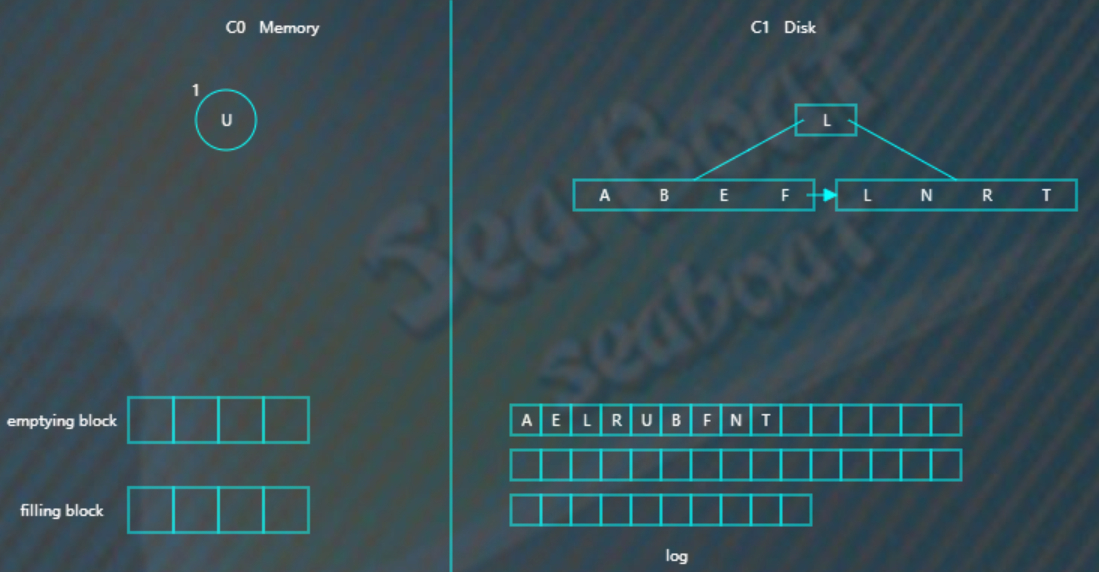
然后将C0树的节点和emptying blcok 合并排序，首先是A进入filling blcok

然后是B

如此类推

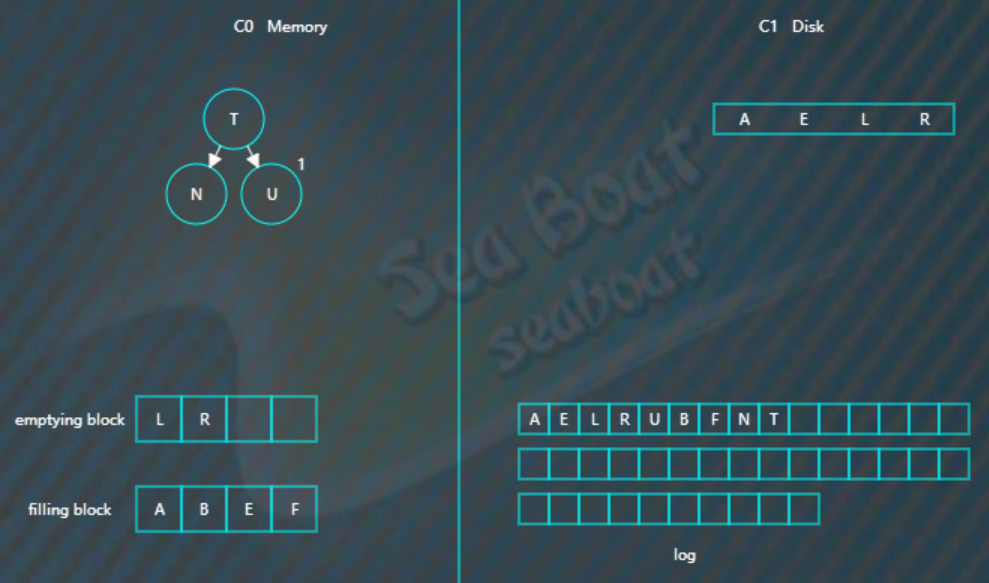
将filling blcok追加到磁盘的新位置，将原来的节点删掉

继续合并，再次填满filling blcok

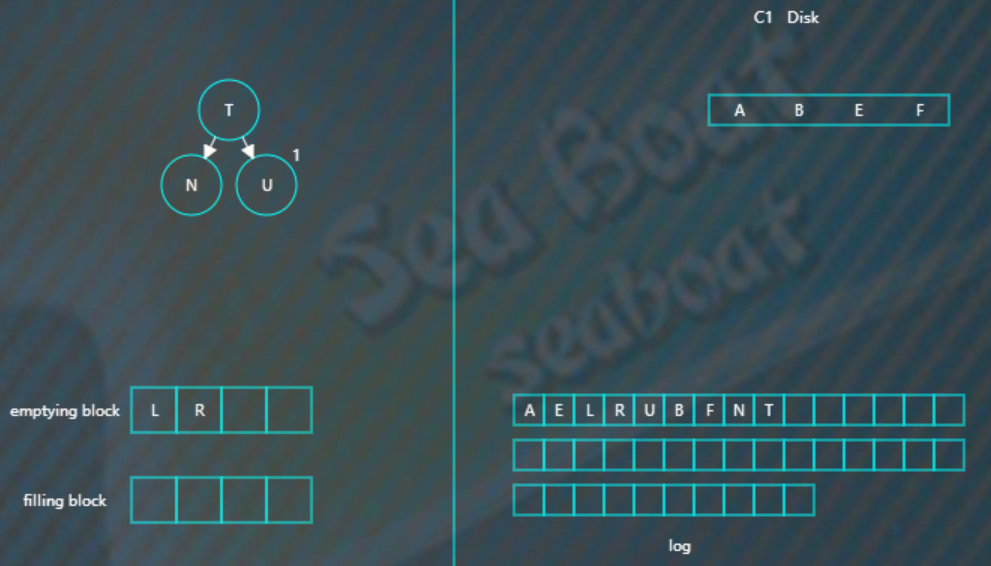
将filling blcok 追加到磁盘的新位置，

查找

总体思想是从最顶层开始查找，如果C0不存在，继续去C1找如此类推。

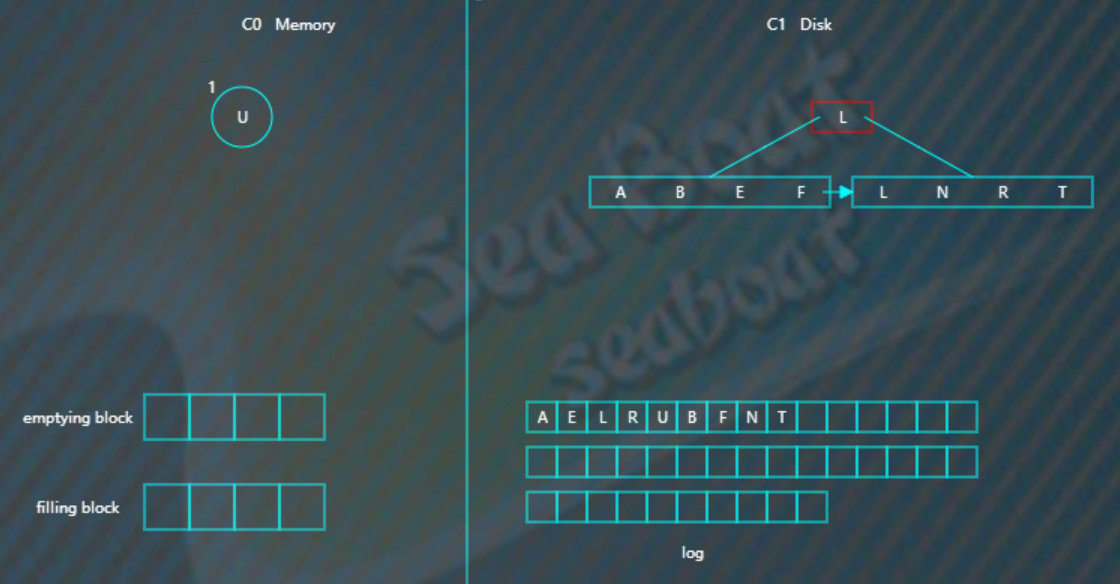
例如要找“B”，从C0开始找没找到

然后找C1树 树根开始找

找到“B”。

删除操作

删除为了能快速执行，标记一下，等下次合并的时候删除相应的记录。

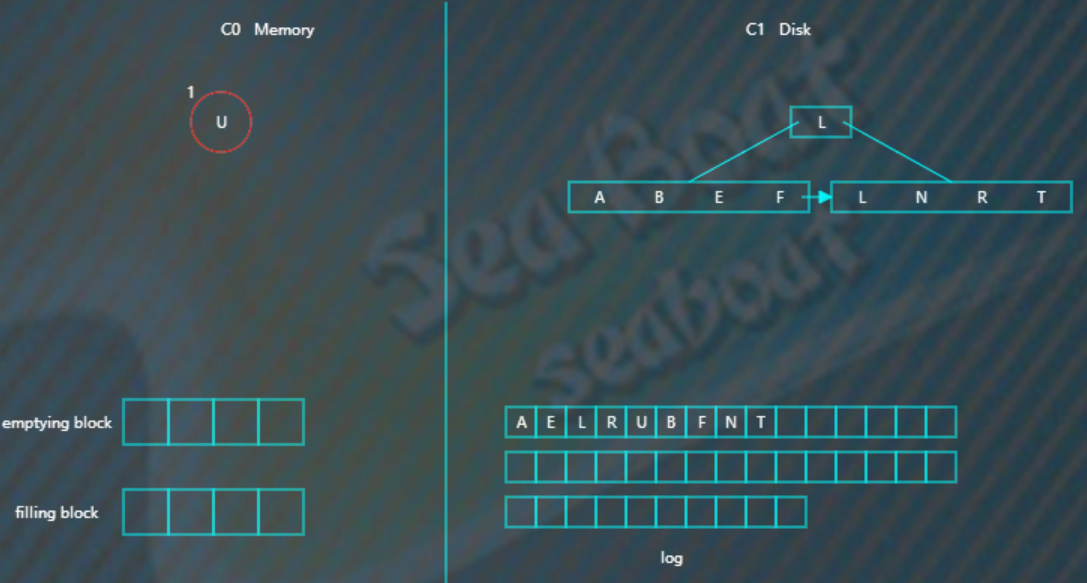
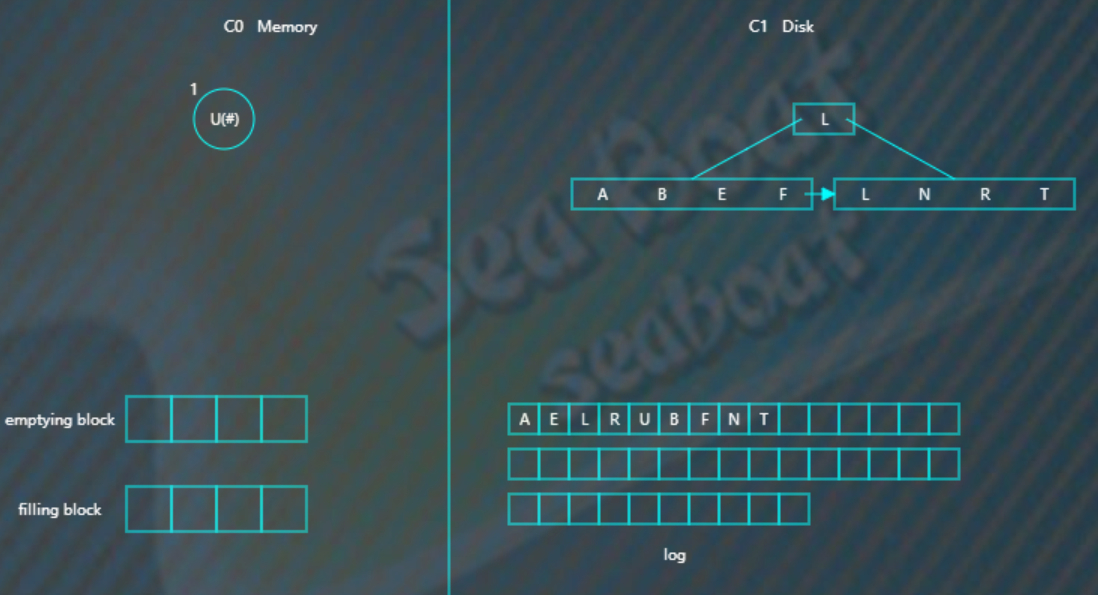
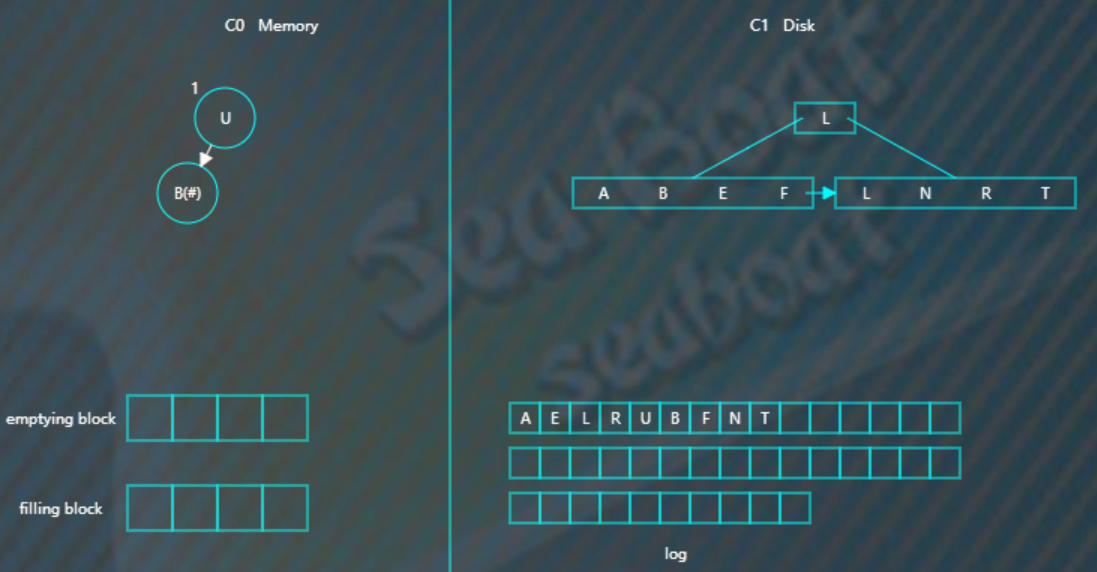
加入要删除“U”，假设标为“#”的表示删除

而如果要删除的key不在C0，则只需要在C0中标志该key已删除，而不需要去硬盘查找。